Authors: Hiroyuki Kasai, Bamdev Mishra, Hiroyuki Sato, Pratik Jawanpuria
Last page update: October 10, 2022
Latest version: 1.0.4 (see Release notes for more info)
Let f: M -> R be a smooth real-valued function on a Riemannian manifold M. The target problem concerns a given model variable w on M, and is expressed as min_{w in M} f(w) := 1/n sum_{i=1}^n f_i(w), where n is the total number of the elements.
This problem has many applications; for example, in principal component analysis (PCA) and the subspace tracking problem, which is the set of r-dimensional linear subspaces in R^d. The low-rank matrix comletion problem and tensor completion problem are promising applications concerning the manifold of fixed-rank matrices/tensors. The linear regression problem is also defined on the manifold of fixed-rank matrices.
A popular choice of algorithms for solving this probem is the Riemannian gradient descent method, which calculates the Riemannian full gradient estimation for every iteration. However, this estimation is computationally costly when n is extremely large. A popular alternative is the Riemannian stochastic gradient descent algorithm (R-SGD), which extends the stochastic gradient descent algorithm (SGD) in the Euclidean space to the Riemannian manifold. As R-SGD calculates only one gradient for the i-th sample, the complexity per iteration is independent of the sample size n. Although R-SGD requires retraction and vector transport operations in every iteration, those calculation costs can be ignored when they are lower than those of the stochastic gradient; this applies to many important Riemannian optimization problems, including the low-rank tensor completion problem and the Riemannian centroid problem.
Similar to SGD, R-SGD is hindered by a slow convergence rate due to a decaying step size sequence. To accelerate the rate of R-SGD, the Riemannian stochastic variance reduced gradient algorithm (R-SVRG) has been proposed; this technique reduces the variance of the stochastic gradient exploiting the finite-sum based on recent progress in variance reduction methods in the Euclidean space . One distinguished feature is reduction of the variance of noisy stochastic gradients by periodical full gradient estimations, which yields a linear convergence rate. Riemannian stochastic quasi-Newton algorithm with variance reduction algorithm (R-SQN-VR) has also recently been proposed, where a stochastic quasi-Newton algorithm and the variance reduced methods are mutually combined. Furthermore, the Riemannian stochastic recursive gradient algorithm (R-SRG) has recently been also proposed to accelerate the convergence rate of R-SGD.
This RSOpt package provides the MATLAB implementation codes dedicated to those stochastic algorithms above.
Note that various manifold algrithms on various manifolds are implemented in MATLAB toolbox manopt. The RSOpt codes are compliant to manopt. Also, please see here for more comprehensive explanation of optimization algorithms on matrix manifolds.
-
R-SGD (Riemannian stochastic gradient descent) algorithm
- S.Bonnabel, "Stochastic gradient descent on Riemannian manifolds," IEEE Trans. on Auto. Cont., 2013.
-
R-SVRG (Riemannian stochastic variance reduced gradient) algorithm
- H.Sato, H.Kasai and B.Mishra, "Riemannian stochastic variance reduced gradient with retration and vector transport," SIOPT2019, arXiv2017.
- H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic variance reduced gradient on Grassmann manifold," NIPS workshop OPT2016, 2016.
- H.Zhang, S.J.Reddi and S.Sra, "Fast stochastic optimization on Riemannian manifolds," NIPS2016, 2016.
-
R-SRG (Riemannian stochastic recursive gradient) algorithm
- H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic recursive gradient algorithm," ICML2018, 2018.
-
R-SQN-VR (Riemannian stochastic quasi-Newton algorithm with variance reduction) (Not yet included)
- H.Kasai, H.Sato and B.Mishra, "Riemannian stochastic quasi-Newton algorithm with variance reduction and its convergence analysis," AISTATS2018, 2018.
-
RASA (Riemannian Adaptive Stochastic gradient algorithm on matrix manifolds) (Coming soon!)
- H.Kasai, P.Jawanpuria and B.Mishra, "Riemannian adaptive stochastic gradient algorithms on matrix manifolds," ICML2019, 2019.
-
Sub-RTR (Subsampled Riemannian trust-region (RTR) algorithms)
- H.Kasai and B.Mishra, "Inexact trust-region algorithms on Riemannian manifolds," NeurIPS2018, 2018.
- The code is available at here.
| Item | R-SVRG | R-SRG |
|---|---|---|
| Need no transport vectors from previous iterate | ☐ (Rrequire existence of inverse of retraction for vector transport) | ☑ |
| Need no inverse of retraction | ☐ | ☑ (Computationally efficient, Applicable to a wider range of manifolds) |
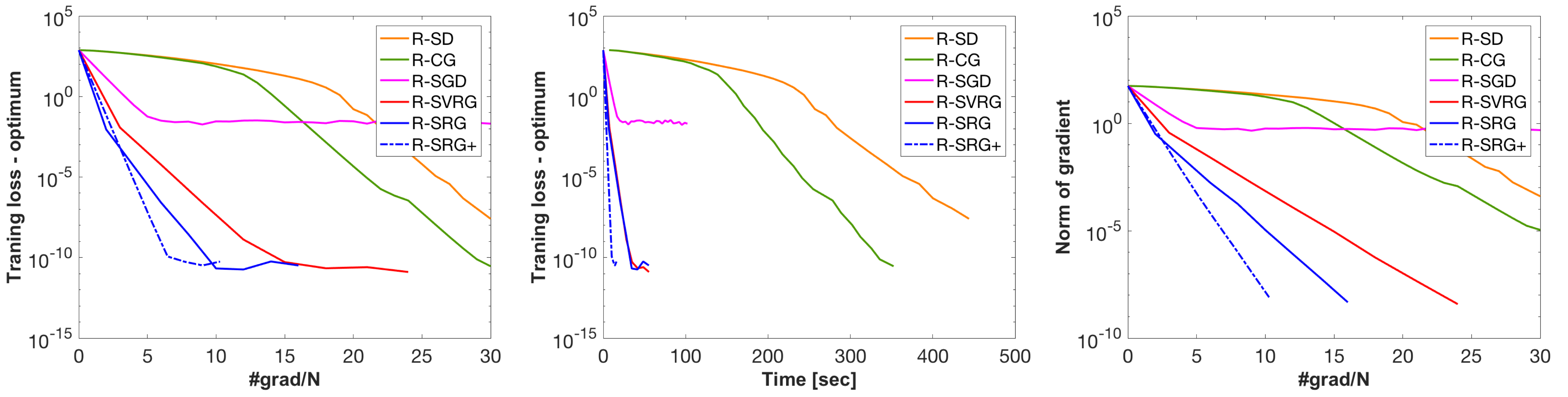
| Accelerated variant | ☐ | ☑ (See More plots below) |
./ - Top directory. ./README.md - This readme file. ./run_me_first.m - The scipt that you need to run first. ./demo.m - Demonstration script to check and understand this package easily. |solvers/ - Contains various Riemannian stochastic optimization algorithms. |tool/ - Some auxiliary tools for this project. |manopt/ - Contains manopt toolbox.
Run run_me_first for path configurations.
%% First run the setup script
run_me_first; Run demo for computing the Riemannian centroid of N symmetric positive-definite (SPD) matrices of size dxd. This problem frequently appears in computer vision
problems such as visual object categorization and pose categorization. This demonstation handles N=500 and d=3.
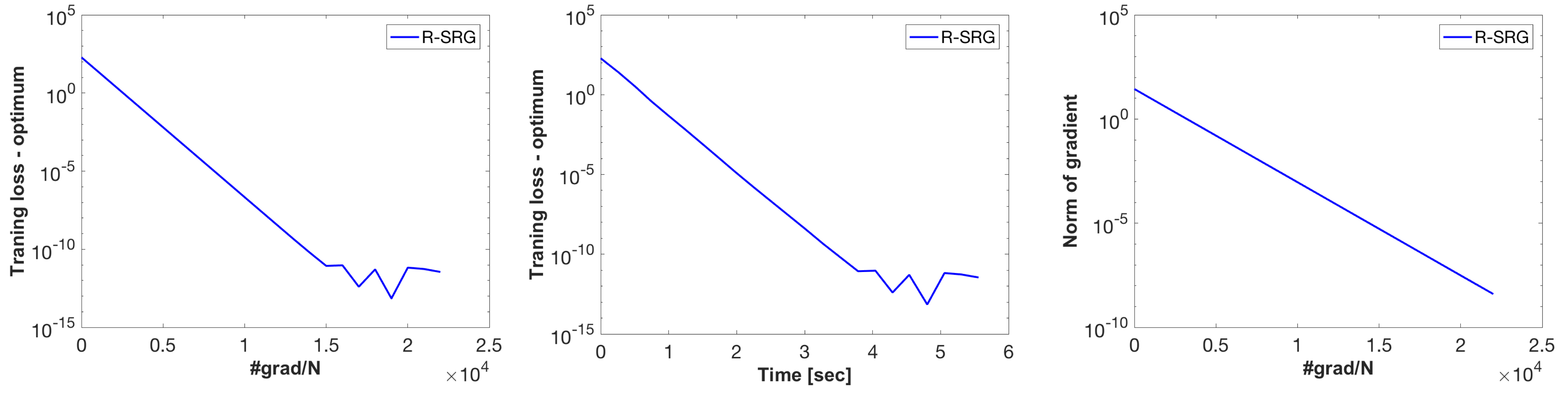
demo; Run show_centroid_plots for the same Riemannian centroid problem. This scripts compares R-SGD, R-SVRG, R-SRG and R-SRG+ as well as batch algorithms including R-SD and R-CG. This scripts handles N=5000 and d=10.
show_centroid_plots; - The code is free and open source.
- The code should only be used for academic/research purposes.
- The code is compliant to MATLAB toolbox manopt.
If you have any problems or questions, please contact the author: Hiroyuki Kasai (email: hiroyuki dot kasai at waseda dot jp)
- Version 1.0.4 (Oct. 10, 2022)
- Readme file is updated.
- Version 1.0.3 (May 31, 2019)
- Some paper informaiton are updated.
- Version 1.0.2 (Sep. 13, 2018)
- MC problem (with Jester dataset) example is added.
- Version 1.0.1 (July 20, 2018)
- Initial codes are available.
- Version 1.0.0 (July 12, 2018)
- Initial version.