Some examples on compressed sensing, inspired by the single pixel camera.
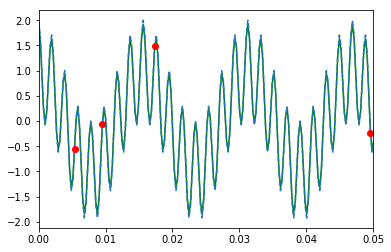
The first example contains a superposition of sine waves (blue) and a set of measurements (red). From these values a reconstruction (green) is generated.
Note that the number of measurements is far below the limit we get from the Nyquist-Shannon sampling theorem.
The second example contains a simple picture of a white blob on black background (right) and a reconstruction from random measurements (left), which represents the way the single pixel camera works.
No work with images is complete without Lena. So I did the same procedure as in the second example but with the usual Lena picture.
The result is a recognizable reconstruction of the original, but not entirely satisfying. I blame the optimization algorithm ¯\_(ツ)_/¯.