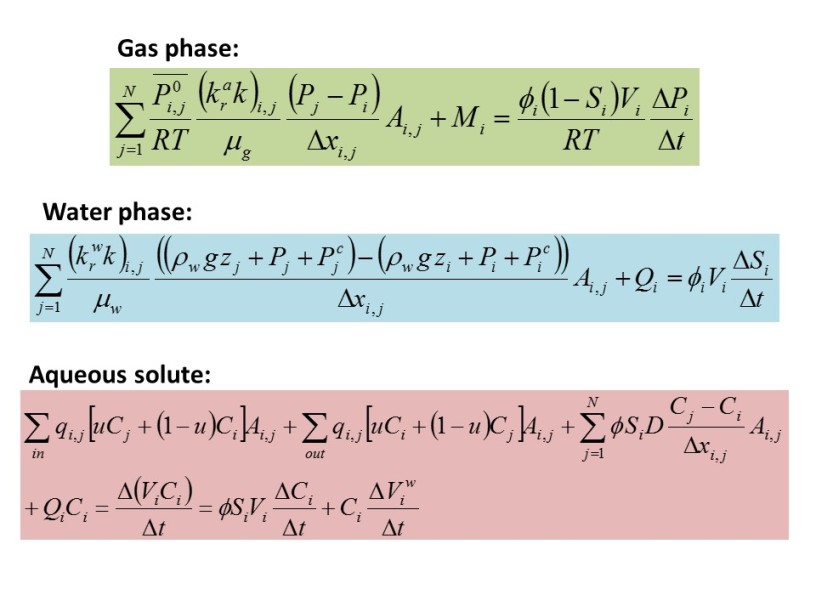
This Julia language (version 0.5) script solves the coupled partial differential equations associated with (1) compressible gas flow in partially water-saturated porous media, (2) partially-saturated flow of water (essentially amounting to a solution of the Richards equation using the Van Genuchten equations for capillarity and relative permeability), and (3) advective-dispersive transport of both aqueous-phase solutes and gas components in the respective media. Currently, exchanges of component mass between phases is not modeled; this feature will be added later when the script is used as the basis for a full multiphase reactive transport model. Other limitations include an isotropic aqueous dispersivity and the neglect of flow driven by density differences.
The model is based on the integral finite difference method, which entails a numerical mesh consisting of arbitrary shapes and properties. The flow and transport equations are solved implicitly with respect to time, using Julia’s built-in sparse matrix algebra capabilities. The following tab-delimited text input files are required to set up and execute the code:
nodes.txt … locations and numbering increment system for nodes (i.e., the volume element centers), properties (volume, permeability, Van Genuchten parameters, links to source terms, dispersivity), fluxes (volumetric for water, and mass for gas) and initial conditions (absolute pressure, water saturation, gas molar fractions, and aqueous component concentrations).
connects.txt … volume element connection information, including index numbers of connecting nodes, numbering increments for additional similar connections, interfacial areas, and node-to-node distances.
knobs.txt … various parameters for running the model (time step constraints, upstream weighting factors). There are comments associated with each parameter within the script.
components.txt … names, gaseous diffusion coefficients, and molecular weights for modeled system components.
source_aqueous.txt and source_gas.txt … source term component compositions (by concentration for aqueous, and by mole fraction for gas).
Two separate example problems are supplied. The top-level folder entails files associated with a steady gas injection scenario in a cylindrical geometry domain (centered about the injection point), with accompanying displacement of water (and a solute tracer) away from the injection point. The resulting transient gas pressure distributions match an analytical solution (see link to blog, below). The “drainage” problem consists simply of gravity-driven percolation of a wetting front in a 1-D column – really just a solution of the Richards equation, with accompanying tracer movement. This problem was used to check mass balance on the solute transport model.
This script is a prototype and has not been tested yet beyond the rudimentary checks noted above. It is intended to be used for more interesting reactive transport problems later, after additional work. Feel free to download and modify, with this caveat in mind. I’d appreciate input on efficiency improvements and bug fixes.
More background information can be found here: https://numericalenvironmental.wordpress.com/2017/01/07/two-phase-reactive-transport-model-development-with-julia-part-2-a-fully-coupled-multicomponent-integral-finite-difference-model/)
An update: I've created an enhanced version of this code that now includes reactive geochemistry. Code and input files are here: https://github.com/NumericalEnvironmental/Coupled_gas_water_transport_with_geochemistry. A little background is here: https://numericalenvironmental.wordpress.com/2017/05/08/two-phase-reactive-transport-model-development-with-julia-part-3-coupling-with-a-geochemical-model/
I'd appreciate hearing back from you if you find the script useful. Questions or comments are welcome at [email protected].
THIS CODE/SOFTWARE IS PROVIDED IN SOURCE OR BINARY FORM "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.