参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
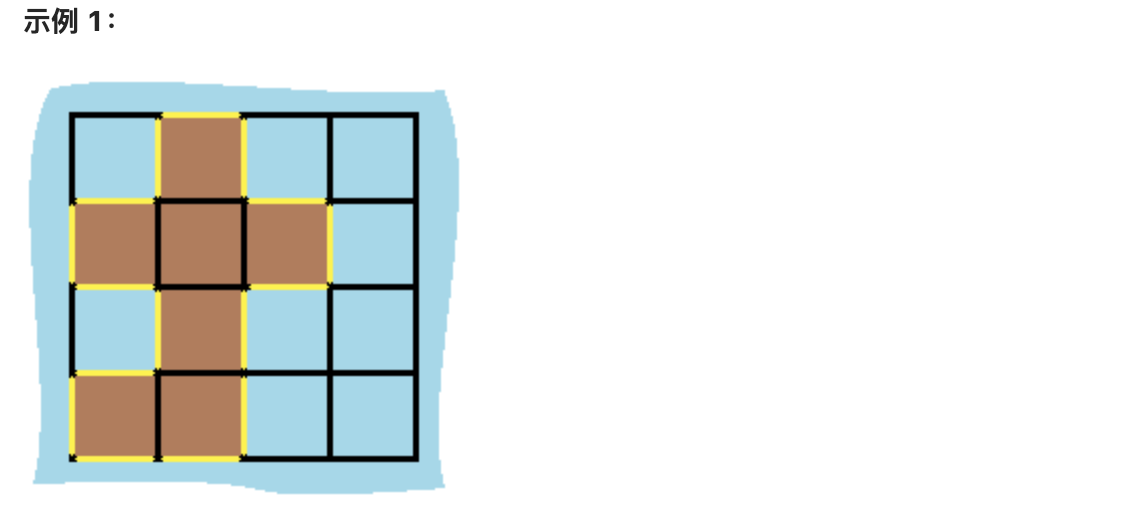
- 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
- 输出:16
- 解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
- 输入:grid = [[1]]
- 输出:4
示例 3:
- 输入:grid = [[1,0]]
- 输出:4
提示:
- row == grid.length
- col == grid[i].length
- 1 <= row, col <= 100
- grid[i][j] 为 0 或 1
岛屿问题最容易让人想到BFS或者DFS,但是这道题还真的没有必要,别把简单问题搞复杂了。
遍历每一个空格,遇到岛屿,计算其上下左右的情况,遇到水域或者出界的情况,就可以计算边了。
如图:
C++代码如下:(详细注释)
class Solution {
public:
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int islandPerimeter(vector<vector<int>>& grid) {
int result = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) { // 上下左右四个方向
int x = i + direction[k][0];
int y = j + direction[k][1]; // 计算周边坐标x,y
if (x < 0 // i在边界上
|| x >= grid.size() // i在边界上
|| y < 0 // j在边界上
|| y >= grid[0].size() // j在边界上
|| grid[x][y] == 0) { // x,y位置是水域
result++;
}
}
}
}
}
return result;
}
};计算出总的岛屿数量,因为有一对相邻两个陆地,边的总数就减2,那么在计算出相邻岛屿的数量就可以了。
result = 岛屿数量 * 4 - cover * 2;
如图:
C++代码如下:(详细注释)
class Solution {
public:
int islandPerimeter(vector<vector<int>>& grid) {
int sum = 0; // 陆地数量
int cover = 0; // 相邻数量
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == 1) {
sum++;
// 统计上边相邻陆地
if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
// 统计左边相邻陆地
if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
// 为什么没统计下边和右边? 因为避免重复计算
}
}
}
return sum * 4 - cover * 2;
}
};// 解法一
class Solution {
// 上下左右 4 个方向
int[] dirx = {-1, 1, 0, 0};
int[] diry = {0, 0, -1, 1};
public int islandPerimeter(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0; // 岛屿周长
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) {
int x = i + dirx[k];
int y = j + diry[k];
// 当前位置是陆地,并且从当前位置4个方向扩展的“新位置”是“水域”或“新位置“越界,则会为周长贡献一条边
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
res++;
continue;
}
}
}
}
}
return res;
}
}
// 解法二
class Solution {
public int islandPerimeter(int[][] grid) {
// 计算岛屿的周长
// 方法二 : 遇到相邻的陆地总周长就-2
int landSum = 0; // 陆地数量
int cover = 0; // 相邻陆地数量
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
landSum++;
// 统计上面和左边的相邻陆地
if(i - 1 >= 0 && grid[i-1][j] == 1) cover++;
if(j - 1 >= 0 && grid[i][j-1] == 1) cover++;
}
}
}
return landSum * 4 - cover * 2;
}
}
// 延伸 - 傳統DFS解法(使用visited數組)(遇到邊界 或是 海水 就edge ++)
class Solution {
int dir[][] ={
{0, 1},
{0, -1},
{1, 0},
{-1, 0}
};
boolean visited[][];
int res = 0;
public int islandPerimeter(int[][] grid) {
int row = grid.length;
int col = grid[0].length;
visited = new boolean[row][col];
int result = 0;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(visited[i][j] == false && grid[i][j] == 1)
result += dfs(grid, i, j);
}
}
return result;
}
private int dfs(int[][] grid, int x, int y){
//如果遇到 邊界(x < 0 || y < 0 || x >= grid.length || y >= grid[0].length)或是 遇到海水(grid[x][y] == 0)就return 1(edge + 1)
if(x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] == 0)
return 1;
//如果該地已經拜訪過,就return 0 避免重複計算
if(visited[x][y])
return 0;
int temp = 0;
visited[x][y] = true;
for(int i = 0; i < 4; i++){
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
//用temp 把edge存起來
temp +=dfs(grid, nextX, nextY);
}
return temp;
}
}扫描每个cell,如果当前位置为岛屿 grid[i][j] == 1, 从当前位置判断四边方向,如果边界或者是水域,证明有边界存在,res矩阵的对应cell加一。
class Solution:
def islandPerimeter(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
# 创建res二维素组记录答案
res = [[0] * n for j in range(m)]
for i in range(m):
for j in range(len(grid[i])):
# 如果当前位置为水域,不做修改或reset res[i][j] = 0
if grid[i][j] == 0:
res[i][j] = 0
# 如果当前位置为陆地,往四个方向判断,update res[i][j]
elif grid[i][j] == 1:
if i == 0 or (i > 0 and grid[i-1][j] == 0):
res[i][j] += 1
if j == 0 or (j >0 and grid[i][j-1] == 0):
res[i][j] += 1
if i == m-1 or (i < m-1 and grid[i+1][j] == 0):
res[i][j] += 1
if j == n-1 or (j < n-1 and grid[i][j+1] == 0):
res[i][j] += 1
# 最后求和res矩阵,这里其实不一定需要矩阵记录,可以设置一个variable res 记录边长,舍矩阵无非是更加形象而已
ans = sum([sum(row) for row in res])
return ansfunc islandPerimeter(grid [][]int) int {
m, n := len(grid), len(grid[0])
res := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 1 {
res += 4
// 上下左右四个方向
if i > 0 && grid[i-1][j] == 1 {res--} // 上边有岛屿
if i < m-1 && grid[i+1][j] == 1 {res--} // 下边有岛屿
if j > 0 && grid[i][j-1] == 1 {res--} // 左边有岛屿
if j < n-1 && grid[i][j+1] == 1 {res--} // 右边有岛屿
}
}
}
return res
}//解法一
var islandPerimeter = function(grid) {
// 上下左右 4 个方向
const dirx = [-1, 1, 0, 0], diry = [0, 0, -1, 1];
const m = grid.length, n = grid[0].length;
let res = 0; //岛屿周长
for(let i = 0; i < m; i++){
for(let j = 0; j < n; j++){
if(grid[i][j] === 1){
for(let k = 0; k < 4; k++){ //上下左右四个方向
// 计算周边坐标的x,y
let x = i + dirx[k];
let y = j + diry[k];
// 四个方向扩展的新位置是水域或者越界就会为周长贡献1
if(x < 0 // i在边界上
|| x >= m // i在边界上
|| y < 0 // j在边界上
|| y >= n // j在边界上
|| grid[x][y] === 0){ // (x,y)位置是水域
res++;
continue;
}
}
}
}
}
return res;
};
//解法二
var islandPerimeter = function(grid) {
let sum = 0; // 陆地数量
let cover = 0; // 相邻数量
for(let i = 0; i < grid.length; i++){
for(let j = 0; j <grid[0].length; j++){
if(grid[i][j] === 1){
sum++;
// 统计上边相邻陆地
if(i - 1 >= 0 && grid[i-1][j] === 1) cover++;
// 统计左边相邻陆地
if(j - 1 >= 0 && grid[i][j-1] === 1) cover++;
// 为什么没统计下边和右边? 因为避免重复计算
}
}
}
return sum * 4 - cover * 2;
};TypeScript:
/**
* 方法一:深度优先搜索(DFS)
* @param grid 二维网格地图,其中 grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域
* @returns 岛屿的周长
*/
function islandPerimeter(grid: number[][]): number {
// 处理特殊情况:网格为空或行列数为 0,直接返回 0
if (!grid || grid.length === 0 || grid[0].length === 0) {
return 0;
}
// 获取网格的行数和列数
const rows = grid.length;
const cols = grid[0].length;
let perimeter = 0; // 岛屿的周长
/**
* 深度优先搜索函数
* @param i 当前格子的行索引
* @param j 当前格子的列索引
*/
const dfs = (i: number, j: number) => {
// 如果当前位置超出网格范围,或者当前位置是水域(grid[i][j] === 0),则周长增加1
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] === 0) {
perimeter++;
return;
}
// 如果当前位置已经访问过(grid[i][j] === -1),则直接返回
if (grid[i][j] === -1) {
return;
}
// 标记当前位置为已访问(-1),避免重复计算
grid[i][j] = -1;
// 继续搜索上、下、左、右四个方向
dfs(i + 1, j);
dfs(i - 1, j);
dfs(i, j + 1);
dfs(i, j - 1);
};
// 遍历整个网格,找到第一个陆地格子(grid[i][j] === 1),并以此为起点进行深度优先搜索
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (grid[i][j] === 1) {
dfs(i, j);
break;
}
}
}
return perimeter;
}
/**
* 方法二:遍历每个陆地格子,统计周长
* @param grid 二维网格地图,其中 grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域
* @returns 岛屿的周长
*/
function islandPerimeter(grid: number[][]): number {
// 处理特殊情况:网格为空或行列数为 0,直接返回 0
if (!grid || grid.length === 0 || grid[0].length === 0) {
return 0;
}
// 获取网格的行数和列数
const rows = grid.length;
const cols = grid[0].length;
let perimeter = 0; // 岛屿的周长
// 遍历整个网格
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
// 如果当前格子是陆地(grid[i][j] === 1)
if (grid[i][j] === 1) {
perimeter += 4; // 周长先加上4个边
// 判断当前格子的上方是否也是陆地,如果是,则周长减去2个边
if (i > 0 && grid[i - 1][j] === 1) {
perimeter -= 2;
}
// 判断当前格子的左方是否也是陆地,如果是,则周长减去2个边
if (j > 0 && grid[i][j - 1] === 1) {
perimeter -= 2;
}
}
}
}
return perimeter;
}