参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

343. 整数拆分

力扣题目链接

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。

示例 1:

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。

算法公开课

《代码随想录》算法视频公开课：动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

看到这道题目，都会想拆成两个呢，还是三个呢，还是四个....

我们来看一下如何使用动规来解决。

动态规划

动规五部曲，分析如下：

确定dp数组（dp table）以及下标的含义

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

dp[i]的定义将贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！

确定递推公式

可以想 dp[i]最大乘积是怎么得到的呢？

其实可以从1遍历j，然后有两种渠道得到dp[i].

一个是j * (i - j) 直接相乘。

一个是j * dp[i - j]，相当于是拆分(i - j)，对这个拆分不理解的话，可以回想dp数组的定义。

那有同学问了，j怎么就不拆分呢？

j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。那么从1遍历j，比较(i - j) * j和dp[i - j] * j 取最大的。递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

也可以这么理解，j * (i - j) 是单纯的把整数拆分为两个数相乘，而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。

如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。

所以递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

那么在取最大值的时候，为什么还要比较dp[i]呢？

因为在递推公式推导的过程中，每次计算dp[i]，取最大的而已。

dp的初始化

不少同学应该疑惑，dp[0] dp[1]应该初始化多少呢？

有的题解里会给出dp[0] = 1，dp[1] = 1的初始化，但解释比较牵强，主要还是因为这么初始化可以把题目过了。

严格从dp[i]的定义来说，dp[0] dp[1] 就不应该初始化，也就是没有意义的数值。

拆分0和拆分1的最大乘积是多少？

这是无解的。

这里我只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1，这个没有任何异议！

确定遍历顺序

确定遍历顺序，先来看看递归公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

所以遍历顺序为：

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

注意枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义了。

j的结束条件是 j < i - 1 ，其实 j < i 也是可以的，不过可以节省一步，例如让j = i - 1，的话，其实在 j = 1的时候，这一步就已经拆出来了，重复计算，所以 j < i - 1

至于 i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。

更优化一步，可以这样：

for (int i = 3; i <= n ; i++) {
    for (int j = 1; j <= i / 2; j++) {
        dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
    }
}

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话也是拆成m个近似数组的子数相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是最差也应该是拆成两个相同的可能是最大值。

那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。

至于 “拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了，感兴趣的同学，可以自己证明。

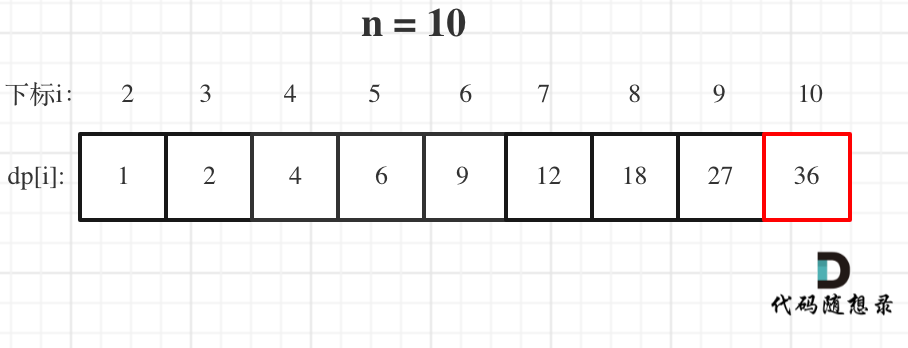
举例推导dp数组

举例当n为10 的时候，dp数组里的数值，如下：

以上动规五部曲分析完毕，C++代码如下：

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            }
        }
        return dp[n];
    }
};

时间复杂度：O(n^2)
空间复杂度：O(n)

贪心

本题也可以用贪心，每次拆成n个3，如果剩下是4，则保留4，然后相乘，但是这个结论需要数学证明其合理性！

我没有证明，而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。

给出我的C++代码如下：

class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

总结

本题掌握其动规的方法，就可以了，贪心的解法确实简单，但需要有数学证明，如果能自圆其说也是可以的。

其实这道题目的递推公式并不好想，而且初始化的地方也很有讲究，我在写本题的时候一开始写的代码是这样的：

class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3) return 1 * (n - 1);
        vector<int> dp(n + 1, 0);
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for (int i = 4; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], dp[i - j] * dp[j]);
            }
        }
        return dp[n];
    }
};

这个代码也是可以过的！

在解释递推公式的时候，也可以解释通，dp[i] 就等于拆解i - j的最大乘积 * 拆解j的最大乘积。看起来没毛病！

但是在解释初始化的时候，就发现自相矛盾了，dp[1]为什么一定是1呢？根据dp[i]的定义，dp[2]也不应该是2啊。

但如果递归公式是 dp[i] = max(dp[i], dp[i - j] * dp[j]);，就一定要这么初始化。递推公式没毛病，但初始化解释不通！

虽然代码在初始位置有一个判断if (n <= 3) return 1 * (n - 1);，保证n<=3 结果是正确的，但代码后面又要给dp[1]赋值1 和 dp[2] 赋值 2，这其实就是自相矛盾的代码，违背了dp[i]的定义！

我举这个例子，其实就说做题的严谨性，上面这个代码也可以AC，大体上一看好像也没有毛病，递推公式也说得过去，但是仅仅是恰巧过了而已。

其他语言版本

Java

class Solution {
    public int integerBreak(int n) {
        //dp[i] 为正整数 i 拆分后的结果的最大乘积
        int[] dp = new int[n+1];
        dp[2] = 1;
        for(int i = 3; i <= n; i++) {
            for(int j = 1; j <= i-j; j++) {
                // 这里的 j 其实最大值为 i-j,再大只不过是重复而已，
                //并且，在本题中，我们分析 dp[0], dp[1]都是无意义的，
                //j 最大到 i-j,就不会用到 dp[0]与dp[1]
                dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
                // j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ，再相乘
                //而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
            }
        }
        return dp[n];
    }
}

Python

动态规划（版本一）

class Solution:
         # 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：
        # 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
        # 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]
    def integerBreak(self, n):
        dp = [0] * (n + 1)   # 创建一个大小为n+1的数组来存储计算结果
        dp[2] = 1  # 初始化dp[2]为1，因为当n=2时，只有一个切割方式1+1=2，乘积为1
       
        # 从3开始计算，直到n
        for i in range(3, n + 1):
            # 遍历所有可能的切割点
            for j in range(1, i // 2 + 1):

                # 计算切割点j和剩余部分(i-j)的乘积，并与之前的结果进行比较取较大值
                
                dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)
        
        return dp[n]  # 返回最终的计算结果

动态规划（版本二）

class Solution:
    def integerBreak(self, n):
        if n <= 3:
            return 1 * (n - 1)  # 对于n小于等于3的情况，返回1 * (n - 1)

        dp = [0] * (n + 1)  # 创建一个大小为n+1的数组来存储最大乘积结果
        dp[1] = 1  # 当n等于1时，最大乘积为1
        dp[2] = 2  # 当n等于2时，最大乘积为2
        dp[3] = 3  # 当n等于3时，最大乘积为3

        # 从4开始计算，直到n
        for i in range(4, n + 1):
            # 遍历所有可能的切割点
            for j in range(1, i // 2 + 1):
                # 计算切割点j和剩余部分(i - j)的乘积，并与之前的结果进行比较取较大值
                dp[i] = max(dp[i], dp[i - j] * dp[j])

        return dp[n]  # 返回整数拆分的最大乘积结果

贪心

class Solution:
    def integerBreak(self, n):
        if n == 2:  # 当n等于2时，只有一种拆分方式：1+1=2，乘积为1
            return 1
        if n == 3:  # 当n等于3时，只有一种拆分方式：1+1+1=3，乘积为1
            return 2
        if n == 4:  # 当n等于4时，有两种拆分方式：2+2=4和1+1+1+1=4，乘积都为4
            return 4
        result = 1
        while n > 4:
            result *= 3  # 每次乘以3，因为3的乘积比其他数字更大
            n -= 3  # 每次减去3
        result *= n  # 将剩余的n乘以最后的结果
        return result

Go

func integerBreak(n int) int {
    /**
    动态五部曲
    1.确定dp下标及其含义
    2.确定递推公式
    3.确定dp初始化
    4.确定遍历顺序
    5.打印dp
    **/
    dp := make([]int, n+1)
    dp[1] = 1
    dp[2] = 1
    for i := 3; i < n+1; i++ {
        for j := 1; j < i-1; j++ {
// i可以差分为i-j和j。由于需要最大值，故需要通过j遍历所有存在的值，取其中最大的值作为当前i的最大值，在求最大值的时候，一个是j与i-j相乘，一个是j与dp[i-j].
            dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]))
        }
    }
    return dp[n]
}
func max(a, b int) int{
    if a > b {
        return a
    }
    return b
}

Javascript

var integerBreak = function(n) {
    let dp = new Array(n + 1).fill(0)
    dp[2] = 1

    for(let i = 3; i <= n; i++) {
        for(let j = 1; j <= i / 2; j++) {
            dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
        }
    }
    return dp[n]
};

Rust

pub fn integer_break(n: i32) -> i32 {
    let n = n as usize;
    let mut dp = vec![0; n + 1];
    dp[2] = 1;
    for i in 3..=n {
        for j in 1..i-1 {
            dp[i] = dp[i].max((i - j) * j).max(dp[i - j] * j);
        }
    }
    dp[n] as i32
}

贪心：

impl Solution {
    pub fn integer_break(mut n: i32) -> i32 {
        match n {
            2 => 1,
            3 => 2,
            4 => 4,
            5.. => {
                let mut res = 1;
                while n > 4 {
                    res *= 3;
                    n -= 3;
                }
                res * n
            }
            _ => panic!("Error"),
        }
    }
}

TypeScript

function integerBreak(n: number): number {
    /**
        dp[i]: i对应的最大乘积
        dp[2]: 1;
        ...
        dp[i]: max(
            1 * dp[i - 1], 1 * (i - 1),
            2 * dp[i - 2], 2 * (i - 2),
            ..., (i - 2) * dp[2], (i - 2) * 2
        );
     */
    const dp: number[] = new Array(n + 1).fill(0);
    dp[2] = 1;
    for (let i = 3; i <= n; i++) {
        for (let j = 1; j <= i / 2; j++) {
            dp[i] = Math.max(dp[i], j * dp[i - j], j * (i - j));
        }
    }
    return dp[n];
};

C

//初始化DP数组
int *initDP(int num) {
    int* dp = (int*)malloc(sizeof(int) * (num + 1));
    int i;
    for(i = 0; i < num + 1; ++i) {
        dp[i] = 0;
    }
    return dp;
}

//取三数最大值
int max(int num1, int num2, int num3) {
    int tempMax = num1 > num2 ? num1 : num2;
    return tempMax > num3 ? tempMax : num3;
}

int integerBreak(int n){
    int *dp = initDP(n);
    //初始化dp[2]为1
    dp[2] = 1;

    int i;
    for(i = 3; i <= n; ++i) {
        int j;
        for(j = 1; j < i - 1; ++j) {
            //取得上次循环:dp[i]，原数相乘，或j*dp[]i-j] 三数中的最大值
            dp[i] = max(dp[i], j * (i - j), j * dp[i - j]);
        }
    }
    return dp[n];
}

Scala

object Solution {
  def integerBreak(n: Int): Int = {
    var dp = new Array[Int](n + 1)
    dp(2) = 1
    for (i <- 3 to n) {
      for (j <- 1 until i - 1) {
        dp(i) = math.max(dp(i), math.max(j * (i - j), j * dp(i - j)))
      }
    }
    dp(n)
  }
}

PHP

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function integerBreak($n) {
        if($n == 0 || $n == 1) return 0;
        if($n == 2) return 1;

        $dp = [];
        $dp[0] = 0;
        $dp[1] = 0;
        $dp[2] = 1;
        for($i=3;$i<=$n;$i++){
            for($j = 1;$j <= $i/2; $j++){
                $dp[$i] = max(($i-$j)*$j, $dp[$i-$j]*$j, $dp[$i]);
            }
        }

        return $dp[$n];
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

0343.整数拆分.md

0343.整数拆分.md

343. 整数拆分

算法公开课

思路

动态规划

贪心

总结

其他语言版本

Java

Python

Go

Javascript

Rust

TypeScript

C

Scala

PHP

Files

0343.整数拆分.md

Latest commit

History

0343.整数拆分.md

File metadata and controls

343. 整数拆分

算法公开课

思路

动态规划

贪心

总结

其他语言版本

Java

Python

Go

Javascript

Rust

TypeScript

C

Scala

PHP