cs229-representer-function.md

CS229 课程讲义中文翻译

CS229 Supplementary notes

原作者	翻译
John Duchi	XiaoDong_Wang

相关链接
Github 地址
知乎专栏
斯坦福大学 CS229 课程网站
网易公开课中文字幕视频

表示函数

1. 广义损失函数

基于我们对监督学习的理解可知学习步骤：

• $(1)$选择问题的表示形式，
• $(2)$选择损失函数，
• $(3)$最小化损失函数。

让我们考虑一个稍微通用一点的监督学习公式。在我们已经考虑过的监督学习设置中，我们输入数据$x \in \mathbb{R}^{n}$和目标$y$来自空间$\mathcal{Y}$。在线性回归中，相应的$y \in \mathbb{R}$，即$\mathcal{Y}=\mathbb{R}$。在logistic回归等二元分类问题中，我们有$y \in \mathcal{Y}={-1,1}$，对于多标签分类问题，我们对于分类数为$k$的问题有$y \in \mathcal{Y}={1,2, \ldots, k}$。

对于这些问题，我们对于某些向量$\theta$基于$\theta^Tx$做了预测，我们构建了一个损失函数$\mathrm{L} : \mathbb{R} \times \mathcal{Y} \rightarrow \mathbb{R}$，其中$\mathrm{L}\left(\theta^{T} x, y\right)$用于测量我们预测$\theta^Tx$时的损失，对于logistic回归，我们使用logistic损失函数：

$$ \mathrm{L}(z, y)=\log \left(1+e^{-y z}\right) \text { or } \mathrm{L}\left(\theta^{T} x, y\right)=\log \left(1+e^{-y \theta^{T} x}\right) $$

对于线性回归，我们使用平方误差损失函数：

$$ \mathrm{L}(z, y)=\frac{1}{2}(z-y)^{2} \quad \text { or } \quad \mathrm{L}\left(\theta^{T} x, y\right)=\frac{1}{2}\left(\theta^{T} x-y\right)^{2} $$

对于多类分类，我们有一个小的变体，其中我们对于$\theta_{i} \in \mathbb{R}^{n}$来说令$\Theta=\left[\theta_{1} \cdots \theta_{k}\right]$，并且使用损失函数$\mathrm{L} : \mathbb{R}^{k} \times{1, \ldots, k} \rightarrow \mathbb{R}$：

$$ \mathrm{L}(z, y)=\log \left(\sum_{i=1}^{k} \exp \left(z_{i}-z_{y}\right)\right) \operatorname{or} \mathrm{L}\left(\Theta^{T} x, y\right)=\log \left(\sum_{i=1}^{k} \exp \left(x^{T}\left(\theta_{i}-\theta_{y}\right)\right)\right) $$

这个想法是我们想要对于所有$i \neq k$得到$\theta_{y}^{T} x>\theta_{i}^{T}$。给定训练集合对$\left{x^{(i)}, y^{(i)}\right}$，通过最小化下面式子的经验风险来选择$\theta$：

$$ J(\theta)=\frac{1}{m} \sum_{i=1}^{m} L\left(\theta^{T} x^{(i)}, y^{(i)}\right)\qquad\qquad(1) $$

2 表示定理

让我们考虑一个稍微不同方法来选择$\theta$使得等式$(1)$中的风险最小化。在许多情况下——出于我们将在以后的课程中学习更多的原因——将正则化添加到风险$J$中是很有用的。我们添加正则化的原因很多：通常它使问题$(1)$容易计算出数值解，它还可以让我们使得等式$(1)$中的风险最小化而选择的$\theta$够推广到未知数据。通常，正则化被认为是形式$r(\theta)=|\theta|$ 或者 $r(\theta)=|\theta|^{2}$其中$|\cdot|$是$\mathbb{R}^{n}$中的范数。最常用的正则化是$l_2$-正则化，公式如下：

$$ r(\theta)=\frac{\lambda}{2}|\theta|_{2}^{2} $$

其中$|\theta|_{2}=\sqrt{\theta^{T} \theta}$被称作向量$\theta$的欧几里得范数或长度。基于此可以得到正规化风险：

$$ J_{\lambda}(\theta)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}\left(\theta^{T} x^{(i)}, y^{(i)}\right)+\frac{\lambda}{2}|\theta|_{2}^{2}\qquad\qquad(2) $$

让我们考虑使得等式$(2)$中的风险最小化而选择的$\theta$的结构。正如我们通常做的那样，我们假设对于每一个固定目标值$y \in \mathcal{Y}$，函数$\mathrm{L}(z, y)$是关于$z$的凸函数。（这是线性回归、二元和多级逻辑回归的情况，以及我们将考虑的其他一些损失。）结果表明，在这些假设下，我们总是可以把问题$(2)$的解写成输入变量$x^{(i)}$的线性组合。更准确地说，我们有以下定理，称为表示定理。

定理2.1 假设在正规化风险$(2)$的定义中有$\lambda\ge 0$。然后，可以得到令正则化化风险$(2)$最小化的式子：

$$ \theta=\sum_{i=1}^{m} \alpha_{i} x^{(i)} $$

其中$\alpha_i$为一些实值权重。

证明 为了直观，我们给出了在把$\mathrm{L}(x,y)$看做关于$z$的可微函数，并且$\lambda>0$的情况下结果的证明。详情见附录A，我们给出了定理的一个更一般的表述以及一个严格的证明。

令$\mathrm{L}^{\prime}(z, y)=\frac{\partial}{\partial z} L(z, y)$代表损失函数关于$z$的导致。则根据链式法则，我们得到了梯度恒等式：

$$ \nabla_{\theta} \mathrm{L}\left(\theta^{T} x, y\right)=\mathrm{L}^{\prime}\left(\theta^{T} x, y\right) x \text { and } \nabla_{\theta} \frac{1}{2}|\theta|_{2}^{2}=\theta $$

其中$\nabla_{\theta}$代表关于$\theta$的梯度。由于风险在所有固定点（包括最小值点）的梯度必须为$0$，我们可以这样写：

$$ \nabla J_{\lambda}(\theta)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}^{\prime}\left(\theta^{T} x^{(i)}, y^{(i)}\right) x^{(i)}+\lambda \theta=\overrightarrow{0} $$

特别的，令$w_{i}=\mathrm{L}^{\prime}\left(\theta^{T} x^{(i)}, y^{(i)}\right)$，因为$\mathrm{L}^{\prime}\left(\theta^{T} x^{(i)}, y^{(i)}\right)$是一个标量（依赖于$\theta$，但是无论$\theta$是多少，$w_i$始终是一个实数），所以我们有：

$$ \theta=-\frac{1}{\lambda} \sum_{i=1}^{n} w_{i} x^{(i)} $$

设$\alpha_{i}=-\frac{w_{i}}{\lambda}$以得到结果。

3 非线性特征与核

基于表示定理$2.1$我们看到，我们可以写出向量$\theta$的作为数据$\left{x^{(i)}\right}_{i=1}^{m}$的线性组合。重要的是，这意味着我们总能做出预测：

$$ \theta^{T} x=x^{T} \theta=\sum_{i=1}^{m} \alpha_{i} x^{T} x^{(i)} $$

也就是说，在任何学习算法中，我们都可以将$\theta^{T} x$替换成$\sum_{i=1}^{m} \alpha_{i} x^{(i)^{T}}x$，然后直接通过$\alpha \in \mathbb{R}^{m}$使其最小化。

让我们从更普遍的角度来考虑这个问题。在我们讨论线性回归时，我们遇到一个问题，输入$x$是房子的居住面积，我们考虑使用特征$x$，$x^2$和$x^3$（比方说）来进行回归，得到一个三次函数。为了区分这两组变量，我们将“原始”输入值称为问题的输入属性（在本例中，$x$是居住面积）。当它被映射到一些新的量集，然后传递给学习算法时，我们将这些新的量称为输入特征。（不幸的是，不同的作者使用不同的术语来描述这两件事，但是我们将在本节的笔记中始终如一地使用这个术语。）我们还将让$\phi$表示特征映射，映射属性的功能。例如，在我们的例子中，我们有：

$$ \phi(x)=\left[ \begin{array}{c}{x} \ {x^{2}} \ {x^{3}}\end{array}\right] $$

与其使用原始输入属性$x$应用学习算法，不如使用一些特征$\phi(x)$来学习。要做到这一点，我们只需要回顾一下之前的算法，并将其中的$x$替换为$\phi(x)$。

因为算法可以完全用内积$\langle x, z\rangle$来表示，这意味着我们可以将这些内积替换为$\langle\phi(x), \phi(z)\rangle$。特别是给定一个特征映射$\phi$，我们可以将相应核定义为：

$$ K(x, z)=\phi(x)^{T} \phi(z) $$

然后，在我们之前的算法中，只要有$\langle x, z\rangle$，我们就可以用$K(x, z)$替换它，并且现在我们的算法可以使用特征$\phi$来学习。让我们更仔细地写出来。我们通过表示定理（定理2.1）看到我们可以对于一些权重$\alpha_i$写出$\theta=\sum_{i=1}^{m} \alpha_{i} \phi\left(x^{(i)}\right)$。然后我们可以写出（正则化）风险：

$$ \begin{aligned} J_{\lambda}(\theta) &=J_{\lambda}(\alpha) \ &=\frac{1}{m} \sum_{i=1}^{m} L\left(\phi\left(x^{(i)}\right)^{T} \sum_{j=1}^{m} \alpha_{j} \phi\left(x^{(j)}\right), y^{(i)}\right)+\frac{\lambda}{2}\left|\sum_{i=1}^{m} \alpha_{i} \phi\left(x^{(i)}\right)\right|{2}^{2} \ &=\frac{1}{m} \sum{i=1}^{m} L\left(\sum_{j=1}^{m} \alpha_{j} \phi\left(x^{(i)}\right)^{T} \phi\left(x^{(j)}\right), y^{(i)}\right)+\frac{\lambda}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} \phi\left(x^{(i)}\right)^{T} \phi\left(x^{(j)}\right) \ &=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}\left(\sum_{j=1}^{m} \alpha_{j} K\left(x^{(i)}, x^{(j)}\right)+\frac{\lambda}{2} \sum_{i, j} \alpha_{i} \alpha_{i} K\left(x^{(i)}, x^{(j)}\right)\right. \end{aligned} $$

也就是说，我们可以把整个损失函数写成核矩阵的最小值：

$$ K=\left[K\left(x^{(i)}, x^{(j)}\right)\right]_{i, j=1}^{m} \in \mathbb{R}^{m \times m} $$

现在，给定$\phi$，我们可以很容易地通过$\phi(x)$和$\phi(z)$和内积计算$K(x,z)$。但更有趣的是，通常$K(x,z)$可能非常廉价的计算，即使$\phi(x)$本身可能是非常难计算的（可能因为这是一个极高维的向量）。在这样的设置中，通过在我们的算法中一个有效的方法来计算$K(x,z)$，我们可以学习的高维特征空间空间由$\phi$给出，但没有明确的找到或表达向量$\phi(x)$。例如，一些核（对应于无限维的向量$\phi$）包括：

$$ K(x, z)=\exp \left(-\frac{1}{2 \tau^{2}}|x-z|_{2}^{2}\right) $$

称为高斯或径向基函数(RBF)核，适用于任何维数的数据，或最小核（适用于$x\in R$）由下式得：

$$ K(x, z)=\min {x, z} $$

有关这些内核机器的更多信息，请参见支持向量机(SVMs)的课堂笔记。

4 核机器学习的随机梯度下降算法

如果我们定义$K \in \mathbb{R}^{m \times m}$为核矩阵，简而言之，定义向量：

$$ K^{(i)}=\left[ \begin{array}{c}{K\left(x^{(i)}, x^{(1)}\right)} \ {K\left(x^{(i)}, x^{(2)}\right)} \ {\vdots} \ {K\left(x^{(i)}, x^{(m)}\right)}\end{array}\right] $$

其中$K=\left[K^{(1)} K^{(2)} \cdots K^{(m)}\right]$，然后，我们可以将正则化风险写成如下简单的形式：

$$ J_{\lambda}(\alpha)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}\left(K^{(i)^{T}} \alpha, y^{(i)}\right)+\frac{\lambda}{2} \alpha^{T} K \alpha $$

现在，让我们考虑对上述风险$J_{\lambda}$取一个随机梯度。也就是说，我们希望构造一个（易于计算的）期望为$\nabla J_{\lambda}(\alpha)$的随机向量，其没有太多的方差。为此,我们首先计算$J(\alpha)$的梯度。我们通过下式来计算单个损失项的梯度：

$$ \nabla_{\alpha} \mathrm{L}\left(K^{(i)^{T}} \alpha, y^{(i)}\right)=\mathrm{L}^{\prime}\left(K^{(i)^{T}} \alpha, y^{(i)}\right) K^{(i)} $$

而：

$$ \nabla_{\alpha}\left[\frac{\lambda}{2} \alpha^{T} K \alpha\right]=\lambda K \alpha=\lambda \sum_{i=1}^{m} K^{(i)} \alpha_{i} $$

因此我们可得：

$$ \nabla_{\alpha} J_{\lambda}(\alpha)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}^{\prime}\left(K^{(i)^{T}} \alpha, y^{(i)}\right) K^{(i)}+\lambda \sum_{i=1}^{m} K^{(i)} \alpha_{i} $$

因此，如果我们选择一个随机索引 ，我们有下式：

$$ \mathrm{L}^{\prime}\left(K^{(i)^{T}} \alpha, y^{(i)}\right) K^{(i)}+m \lambda K^{(i)} \alpha_{i} $$

上式是关于$J_{\lambda}(\alpha)$的随机梯度。这给我们一个核监督学习问题的随机梯度算法，如图$1$所示。关于算法$1$，有一点需要注意：因为我们为了保持梯度的无偏性而在$\lambda K^{(i)} \alpha_{i}$项上乘了$m$，所以参数$\lambda>0$不能太大，否则算法就会有点不稳定。此外，通常选择的步长是$\eta_{t}=1 / \sqrt{t}$，或者是它的常数倍。

5 支持向量机

现在我们讨论支持向量机(SVM)的一种方法，它适用于标签为$y \in{-1,1}$的二分类问题。并给出了损失函数$\mathrm{L}$的一种特殊选择，特别是在支持向量机中，我们使用了基于边缘的损失函数：

$$ \mathrm{L}(z, y)=[1-y z]_{+}=\max {0,1-y z}\qquad\qquad(3) $$

因此，在某种意义上，支持向量机只是我们前面描述的一般理论结果的一个特例。特别的，我们有经验正则化风险：

$$ J_{\lambda}(\alpha)=\frac{1}{m} \sum_{i=1}^{m}\left[1-y^{(i)} K^{(i)^{T}} \alpha\right]_{+}+\frac{\lambda}{2} \alpha^{T} K \alpha $$

其中矩阵$K=\left[K^{(1)} \cdots K^{(m)}\right]$通过$K_{i j}=K\left(x^{(i)}, x^{(j)}\right)$来定义。

在课堂笔记中，你们可以看到另一种推导支持向量机的方法以及我们为什么称呼其为支持向量机的描述。

6 一个例子

在本节中，我们考虑一个特殊的例子——核，称为高斯或径向基函数(RBF)核。这个核由下式给出：

$$ K(x, z)=\exp \left(-\frac{1}{2 \tau^{2}}|x-z|_{2}^{2}\right)\qquad\qquad(4) $$

其中$\tau>0$是一个控制内核带宽的参数。直观地，当$\tau$非常小时，除非$x \approx z$我们将得到$K(x, z) \approx 0$。即$x$和$z$非常接近，在这种情况下我们有$K(x, z) \approx 1$。然而，当$\tau$非常大时，则我们有一个更平滑的核函数$K$。这个核的功能函数$\phi$是在无限维$^1$的空间中。即便如此，通过考虑一个新的例子$x$所做的分类，我们可以对内核有一些直观的认识：我们预测：

上一小段上标1的说明（详情请点击本行）

如果你看过特征函数或者傅里叶变换，那么你可能会认出RBF核是均值为零，方差为$\tau^{2}$的高斯分布的傅里叶变换。也就是在$\mathbb{R}^{n}$中令$W\sim \mathrm{N}\left(0, \tau^{2} I_{n \times n}\right)$，使得$W$的概率密函数为$p(w)=\frac{1}{\left(2 \pi \tau^{2}\right)^{n / 2}} \exp \left(-\frac{|w|_{2}^{2}}{2 \tau^{2}}\right)$。令$i=\sqrt{-1}$为虚数单位，则对于任意向量$v$我们可得：

$$ \begin{aligned} \mathbb{E}\left[\exp \left(i v^{T} W\right)\right] =\int \exp \left(i v^{T} w\right) p(w) d w &=\int \frac{1}{\left(2 \pi \tau^{2}\right)^{n / 2}} \exp \left(i v^{T} w-\frac{1}{2 \tau^{2}}|w|{2}^{2}\right) d w \ &=\exp \left(-\frac{1}{2 \tau^{2}}|v|{2}^{2}\right) \end{aligned} $$

因此，如果我们定义“向量”（实际上是函数）$\phi(x, w)=e^{i x^{T} w}$并令$a^*$是$a \in \mathbb{C}$的共轭复数，则我们可得：

$$ \mathbb{E}\left[\phi(x, W) \phi(z, W)^{*}\right]=\mathbb{E}\left[e^{i x^{T} W} e^{-i x^{T} W}\right]=\mathbb{E}\left[\exp \left(i W^{T}(x-z)\right)\right]=\exp \left(-\frac{1}{2 \tau^{2}}|x-z|_{2}^{2}\right) $$

特别地，我们看到$K(x, z)$是一个函数空间的内积这个函数空间可以对$p(w)$积分。

$$ \sum_{i=1}^{m} K\left(x^{(i)}, x\right) \alpha_{i}=\sum_{i=1}^{m} \exp \left(-\frac{1}{2 \tau^{2}}\left|x^{(i)}-x\right|{2}^{2}\right) \alpha{i} $$

所以这就变成了一个权重，取决于$x$离每个$x^{(i)}$有多近，权重的贡献$\alpha_i$乘以$x$到$x^{(i)}$的相似度，由核函数决定。

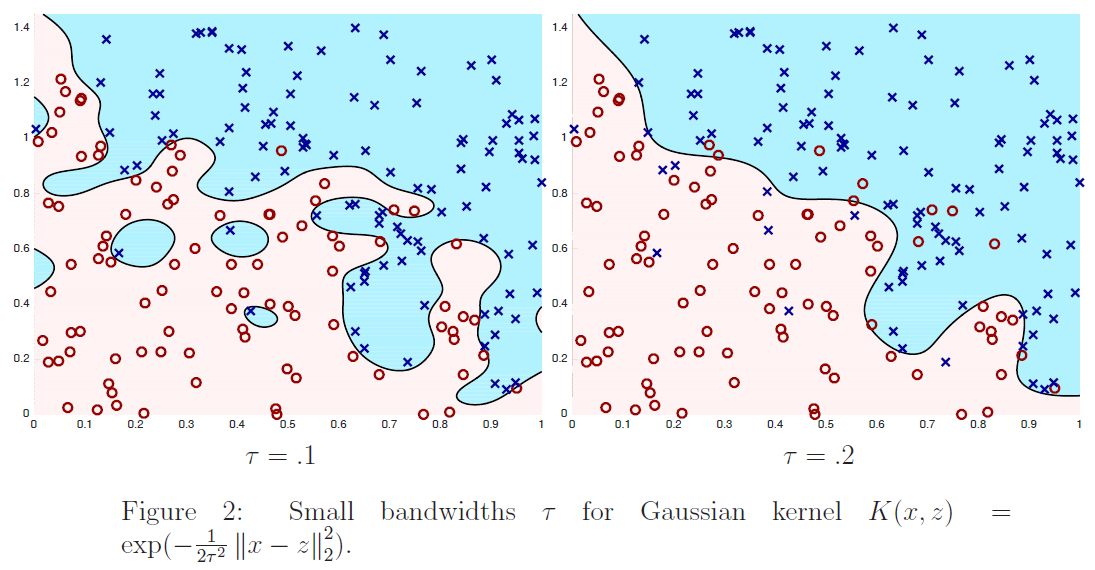
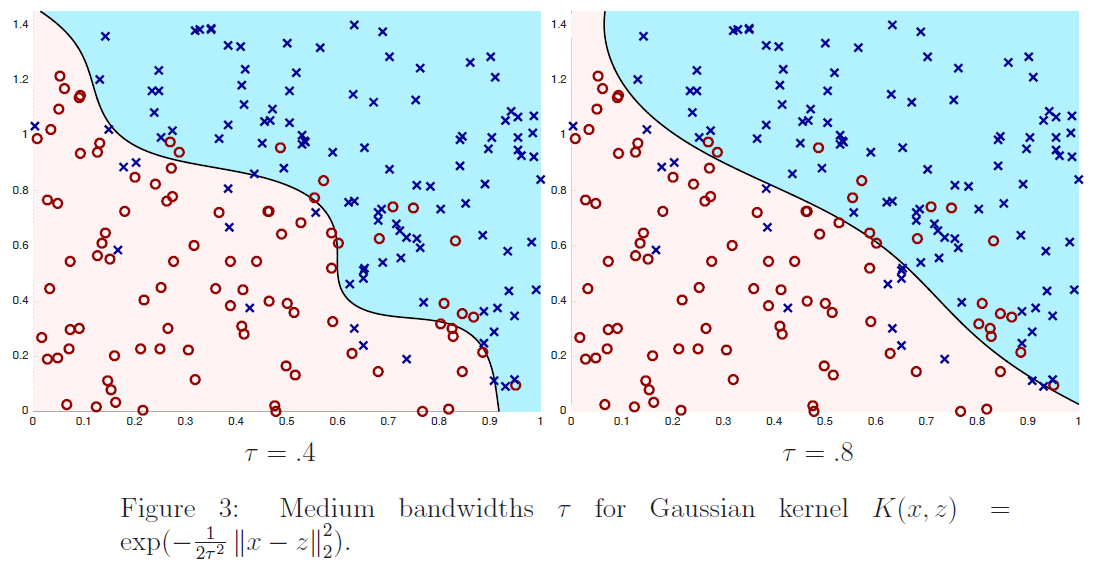
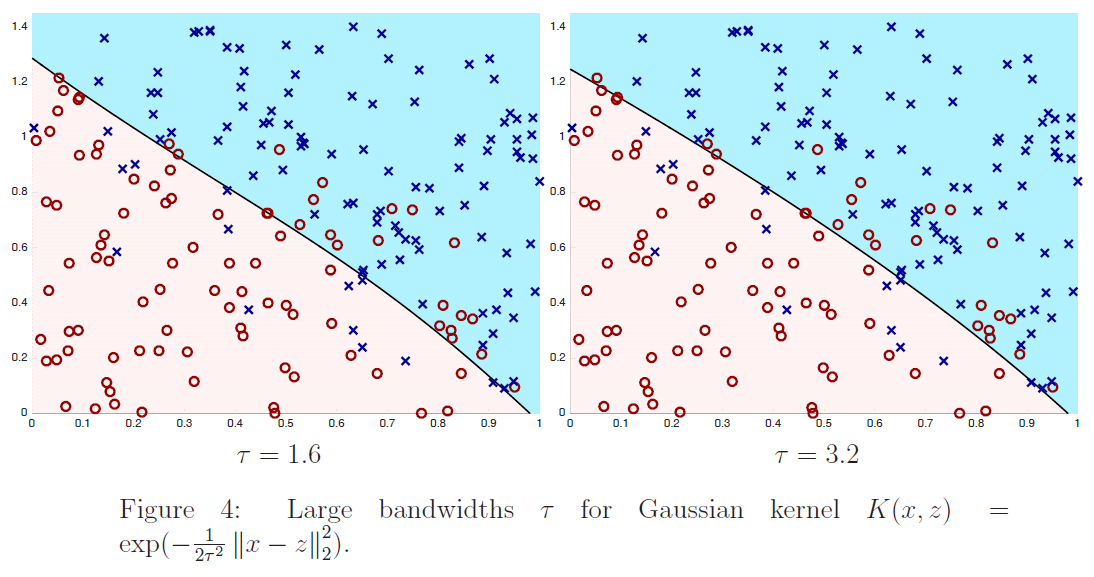
在图$2$、$3$和$4$中，我们通过最小化下式显示了训练$6$个不同内核分类器的结果：

$$ J_{\lambda}(\alpha)=\sum_{i=1}^{m}\left[1-y^{(i)} K^{(i)^{T}} \alpha\right]_{+}+\frac{\lambda}{2} \alpha^{T} K \alpha $$

其中$m=200,\lambda=1/m$，核公式$(4)$中的$\tau$取不同的值。我们绘制了训练数据（正例为蓝色的x，负例为红色的o）以及最终分类器的决策面。也就是说，我们画的线由下式：

$$ \left{x \in \mathbb{R}^{2} : \sum_{i=1}^{m} K\left(x, x^{(i)}\right) \alpha_{i}=0\right} $$

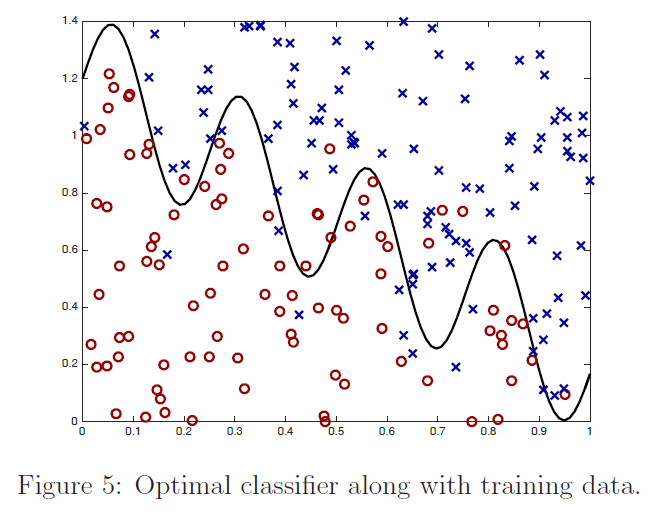
定义给出了学习分类器进行预测$\sum_{i=1}^{m} K\left(x, x^{(i)}\right) \alpha_{i}>0$和$\sum_{i=1}^{m} K\left(x, x^{(i)}\right) \alpha_{i}<0$的区域。从图中我们看到，对于数值较大的$\tau$的一个非常简单的分类器：它几乎是线性的，而对于$τ=.1$，分类器有实质性的变化，是高度非线性的。为了便于参考，在图$5$中，我们根据训练数据绘制了最优分类器；在训练数据无限大的情况下，最优分类器能最大限度地减小误分类误差。

A 一个更一般的表示定理

在这一节中，我们给出了一个更一般版本的表示定理以及一个严格的证明。令$r : \mathbb{R} \rightarrow \mathbb{R}$为任何非降函数的自变量，并考虑正则化风险：

$$ J_{r}(\theta)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}\left(x^{(i)^{T}} \theta, y^{(i)}\right)+r\left(|\theta|_{2}\right)\qquad\qquad(5) $$

通常，我们取$r(t)=\frac{\lambda}{2} t^{2}$，与通常的选择$l_2$-正则化相对应。但是下一个定理表明这对于表示定理来说是不必要的。事实上，我们可以对所有的$t$取$r(t) = 0$，这个定理仍然成立。

定理 A.1 （向量空间$R^n$中的表示定理）。令$\theta \in \mathbb{R}^{n}$为任意向量。则存在$\alpha \in \mathbb{R}^{m}$和$\theta^{(\alpha)}=\sum_{i=1}^{m} \alpha_{i} x^{(i)}$使得：

$$ J_{r}\left(\theta^{(\alpha)}\right) \leq J_{r}(\theta) $$

特别的，没有普遍的损失函数总是假设我们可以最小化$J(\theta)$来写出优化问题，其中最小化$J(\theta)$时仅仅考虑$\theta$在数据的张成的空间中的情况。

证明 我们的证明依赖于线性代数中的一些性质，它允许我们证明简洁，但是如果你觉得太过简洁，请随意提问。

向量$\left{x^{(i)}\right}_{i=1}^{m}$在向量空间$\mathbb{R}^{n}$中。因此有$\mathbb{R}^{n}$中的子空间$V$使得：

$$ V=\left{\sum_{i=1}^{m} \beta_{i} x^{(i)} : \beta_{i} \in \mathbb{R}\right} $$

那么$V$对于向量$v_{i} \in \mathbb{R}^{n}$有一个标准正交基$\left{v_{1}, \dots, v_{n_{0}}\right}$，其中标准正交基的长度（维度）是$n_{0} \leq n$。因此我们可以写出$V=\left{\sum_{i=1}^{n_{0}} b_{i} v_{i}:b_{i} \in \mathbb{R} \right}$，回忆一下正交性是是指向量$v_i$满足$\left|v_{i}\right|{2}=1$和对于任意$i\neq j$有$v{i}^{T} v_{j}=0$。还有一个正交子空间$V^{\perp}=\left{u \in \mathbb{R}^{n} : u^{T} v=0\quad for\quad all\quad v \in V\right}$，其有一个维度是$n_{\perp}=n-n_{0} \geq 0$的正交基，我们可以写作$\left{u_{1}, \ldots, u_{n_{\perp}}\right} \subset \mathbb{R}^{n}$，其对于所有$i,j$都满足$u_{i}^{T} v_{j}=0$。

因为$\theta \in \mathbb{R}^{n}$，我们可以把它唯一地写成：

$$ \theta=\sum_{i=1}^{n_{0}} \nu_{i} v_{i}+\sum_{i=1}^{n_{\perp}} \mu_{i} u_{i}, \quad \text { where } \nu_{i} \in \mathbb{R} \text { and } \mu_{i} \in \mathbb{R} $$

其中$\mu, \nu$的值是唯一的。现在通过$\left{x^{(i)}\right}_{i=1}^{m}$张成的空间$V$的定义可知，存在$\alpha \in \mathbb{R}^{m}$使得：

$$ \sum_{i=1}^{n_{0}} \nu_{i} v_{i}=\sum_{i=1}^{m} \alpha_{i} x^{(i)} $$

因此我们有：

$$ \theta=\sum_{i=1}^{m} \alpha_{i} x^{(i)}+\sum_{i=1}^{n_{\perp}} \mu_{i} u_{i} $$

定义$\theta^{(\alpha)}=\sum_{i=1}^{m} \alpha_{i} x^{(i)}$。现在对于任意数据点$x^{(j)}$，我们有：

$$ u_{i}^{T} x^{(j)}=0 \text { for all } i=1, \ldots, n_{\perp} $$

使得$u_{i}^{T} \theta^{(\alpha)}=0$。因此我们可得：

$$ |\theta|{2}^{2}=\left|\theta^{(\alpha)}+\sum{i=1}^{n_{\perp}} \mu_{i} u_{i}\right|{2}^{2}=\left|\theta^{(\alpha)}\right|{2}^{2}+\underbrace{2 \sum_{i=1}^{n_{\perp}} \mu_{i} u_{i}^{T} \theta^{(\alpha)}}{=0}+\left|\sum{i=1}^{n_{\perp}} \mu_{i} u_{i}\right|{2}^{2} \geq\left|\theta^{(\alpha)}\right|{2}^{2}\quad(6a) $$

同时我们可得：

$$ \theta^{(\alpha)^{T}} x^{(i)}=\theta^{T} x^{(i)}\qquad\qquad(6b) $$

对于所有点$x^{(i)}$都成立。

即，通过使用$|\theta|{2} \geq\left|\theta^{(\alpha)}\right|{2}$以及等式$(6b)$，我们可得：

$$ \begin{aligned} J_{r}(\theta)=\frac{1}{m} \sum_{i=1}^{m} \mathrm{L}\left(\theta^{T} x^{(i)}, y^{(i)}\right)+r\left(|\theta|{2}\right) &\stackrel{(6 \mathrm{b})}{=} \frac{1}{m} \sum{i=1}^{m} \mathrm{L}\left(\theta^{(\alpha)^{T}} x^{(i)}, y^{(i)}\right)+r\left(|\theta|{2}\right)\ &\stackrel{(6 \mathrm{a})}{ \geq} \frac{1}{m} \sum{i=1}^{m} \mathrm{L}\left(\theta^{(\alpha)^{T}} x^{(i)}, y^{(i)}\right)+r\left(\left|\theta^{(\alpha)}\right|{2}\right)\ &=J{r}\left(\theta^{(\alpha)}\right) \end{aligned} $$

这是期望的结果。