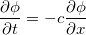README.md

pyranda

A Python driven, Fortran powered Finite Difference solver for arbitrary hyperbolic PDE systems. This is the mini-app for the Miranda code.

The PDE solver defaults to a 10th order compact finite difference method for spatial derivatives, and a 5-stage, 4th order Runge-Kutta scheme for temporal integration. Other numerical methods will be added in the future.

Pyranda parses (through a simple interpreter) the full definition of a system of PDEs, namely:

• a domain and discretization (in 1D, 2D or 3D)
• governing equations written on RHS of time derivatives.
• initial values for all variables
• boundary conditions

Prerequisites

At a minimum, your system will need the following installed to run pyranda. (see install notes for detailed instructions)

• A fortran compiler with MPI support
• python 2.7, including these packages
  • numpy
  • mpi4py

Tutorials

A few tutorials are included on the project wiki page that cover the example below, as well as few others. A great place to start if you want to discover what types of problems you can solve.

Example Usage - Solve the 1D advection equation in less than 10 lines of code

The one-dimensional advection equation is written as:

where phi is a scalar and where c is the advection velocity, assumed to be unity. We solve this equation in 1D, in the x-direction from (0,1) using 100 points and evolve the solution .1 units in time.

1 - Import pyranda

from pyranda import pyrandaSim

2 - Initialize a simulation object on a domain/mesh

pysim = pyrandaSim('advection',"xdom = (0.0 , 1.0 , 100 )")

3 - Define the equations of motion

pysim.EOM(" ddt(:phi:) = - ddx(:phi:) ")

4 - Initialize variables

pysim.setIC(":phi: = 1.0 + 0.1 * exp( -(abs(meshx-.5)/.1 )**2 )")

5 - Integrate in time

dt = .001
time = 0.0
while time < .1:
   time = pysim.rk4(time,dt)

6 - Plot the solution

pysim.plot.plot('phi')