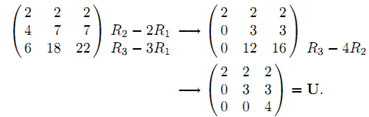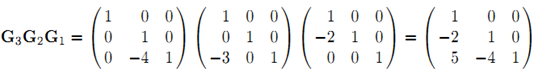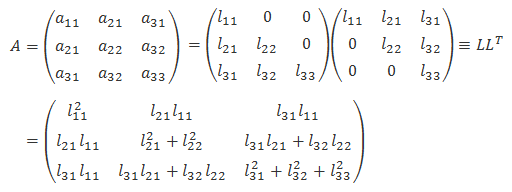Review.md

Probability

Bayes Rule

Bayes network

Scientific Computation

LU 分解

L 为 G₃G₂G₁的矩阵的逆

https://blog.csdn.net/Zijie123pea/article/details/113813747 介绍了 LU 的 L 比较快的求解方法

full pivoting相比partial pivoting更加稳定，但是更麻烦，速度会慢。

Cholesky 分解

Reference:

https://zhuanlan.zhihu.com/p/112091443

https://zhuanlan.zhihu.com/p/84210687

Ax = b 未必线性有解，即 A 不可逆，A^-1无法计算，所以我们希望最小化 || Ax - b||₂

Error 求导

可得

（A^TA）^-1也未必存在逆矩阵（underdetermined），所以才有 Tikhonov regularization

​ A^TA 至少是半正定矩阵

对于正定矩阵（A 的列向量线性无关）有 Cholesky 分解(为 LU 分解的特殊情况)

如

QR 分解

Reference:

https://blog.csdn.net/u010945683/article/details/45972819

SVD 分解

https://zhuanlan.zhihu.com/p/54681618?from_voters_page=true

https://www.cnblogs.com/marsggbo/p/10155801.html

计算过程重点看第二个

非线性系统

Newton’s Method: https://zhuanlan.zhihu.com/p/46536960

Secant’s Method: